λ 演算 | LordYao

Abstract

Keywords

Citation Yao Qing-sheng.λ 演算.FUTURE & CIVILIZATION Natural/Social Philosophy & Infomation Sciences,20240428. https://yaoqs.github.io/20240428/lyan-suan/

Good Math/Bad Math
- cgnail
- 博客推荐：good math, bad math 之 Lambda 算子简介

¶ 我的最爱 Lambda 演算 —— 开篇

15 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

原文来自 Good Math/Bad Math 的系列连载，全文分 7 章，本篇是第 1 章。中文博客负暄琐话对这个系列的前 6 章做过翻译，强迫症表示忍受不了「下面没有了」，于是自己动手做了全套。这里只对原文做了翻译，而 “负暄琐话” 的版本则加上了很多掌故，使得阅读起来更有趣味性。

（在这个帖子的原始版本里，我试图用一个 JavaScript 工具来生成 MathML。但不太顺利：有几个浏览器没法正确的渲染，在 RSS feed 里也显示的不好。所以我只好从头开始，用简单的文本格式重新写一遍。）

计算机科学，尤其是编程语言，经常倾向于使用一种特定的演算：Lambda 演算（Lambda Calculus）。这种演算也广泛地被逻辑学家用于学习计算和离散数学的结构的本质。Lambda 演算伟大的的原因有很多，其中包括：

非常简单。
图灵完备。
容易读写。
语义足够强大，可以从它开始做（任意）推理。
它有一个很好的实体模型。
容易创建变种，以便我们探索各种构建计算或语义方式的属性。

Lambda 演算易于读写，这一点很重要。它导致人们开发了很多极为优秀的编程语言，他们在不同程度上都基于 Lambda 演算：LISP，ML 和 Haskell 语言都极度依赖于 Lambda 演算。

Lambda 演算建立在函数的概念的基础上。纯粹的 Lambda 演算中，一切都是函数，连值的概念都没有。但是，我们可以用函数构建任何我们需要的东西。还记得在这个博客的初期，我谈了一些关于如何建立数学的方法么？我们可以从无到有地用 Lambda 演算建立数学的整个结构。

闲话少说，让我们深入的看一看 LC（Lambda Calculus）。对于一个演算，需要定义两个东西：语法，它描述了如何在演算中写出合法的表达式；一组规则，让你符号化地操纵表达式。

¶Lambda 演算的语法

Lambda 演算只有三类表达式：

函数定义：Lambda 演算中的函数是一个表达式，写成：lambda x . body，表示 “一个参数参数为 x 的函数，它的返回值为 body 的计算结果。” 这时我们说：Lambda 表达式绑定了参数 x。
标识符引用（Identifier reference）：标识符引用就是一个名字，这个名字用于匹配函数表达式中的某个参数名。
函数应用（Function application）：函数应用写成把函数值放到它的参数前面的形式，如 (lambda x . plus x x) y。

¶ 柯里化

在 Lambda 演算中有一个技巧：如果你看一下上面的定义，你会发现一个函数（Lambda 表达式）只接受一个参数。这似乎是一个很大的局限 —— 你怎么能在只有一个参数的情况下实现加法？

这一点问题都没有，因为函数就是值。你可以写只有一个参数的函数，而这个函数返回一个带一个参数的函数，这样就可以实现写两个参数的函数了 —— 本质上两者是一样的。这就是所谓的柯里化（Currying），以伟大的逻辑学家 Haskell Curry 命名。

例如我们想写一个函数来实现 x + y。我们比较习惯写成类似：lambda x y . plus x y 之类的东西。而采用单个参数函数的写法是：我们写一个只有一个参数的函数，让它返回另一个只有一个参数的函数。于是 x + y 就变成一个单参数 x 的函数，它返回另一个函数，这个函数将 x 加到它自己的参数上：

1	lambda x. ( lambda y. plus x y )

现在我们知道，添加多个参数的函数并没有真正添加任何东西，只不过简化了语法，所以下面继续介绍的时候，我会在方便的时候用到多参数函数。

¶ 自由标识符 vs. 绑定标识符

有一个重要的语法问题我还没有提到：闭包（closure）或者叫完全绑定（complete binding）。在对一个 Lambda 演算表达式进行求值的时候，不能引用任何未绑定的标识符。如果一个标识符是一个闭合 Lambda 表达式的参数，我们则称这个标识符是（被）绑定的；如果一个标识符在任何封闭上下文中都没有绑定，那么它被称为自由变量。

lambda x . plus x y：在这个表达式中，y 和 plus 是自由的，因为他们不是任何闭合的 Lambda 表达式的参数；而 x 是绑定的，因为它是函数定义的闭合表达式 plus x y 的参数。
lambda x y . y x ：在这个表达式中 x 和 y 都是被绑定的，因为它们都是函数定义中的参数。
lambda y . (lambda x . plus x y)：在内层演算 lambda x . plus x y 中，y 和 plus 是自由的，x 是绑定的。在完整表达中，x 和 y 是绑定的：x 受内层绑定，而 y 由剩下的演算绑定。plus 仍然是自由的。

我们会经常使用 free(x) 来表示在表达式 x 中自由的标识符。

一个 Lambda 演算表达式只有在其所有变量都是绑定的时候才完全合法。但是，当我们脱开上下文，关注于一个复杂表达式的子表达式时，自由变量是允许存在的 —— 这时候搞清楚子表达式中的哪些变量是自由的就显得非常重要了。

¶Lambda 演算运算法则

Lambda 演算只有两条真正的法则：称为 Alpha 和 Beta。Alpha 也被称为「转换」，Beta 也被称为「规约」。

¶Alpha 转换

Alpha 是一个重命名操作；基本上就是说，变量的名称是不重要的：给定 Lambda 演算中的任意表达式，我们可以修改函数参数的名称，只要我们同时修改函数体内所有对它的自由引用。

所以 —— 例如，如果有这样一个表达式：

1	lambda x . if (= x 0) then 1 else x ^ 2

我们可以用 Alpha 转换，将 x 变成 y（写作 alpha[x / y]），于是我们有：

1	lambda y . if (= y 0) then 1 else y ^ 2

这样丝毫不会改变表达式的含义。但是，正如我们将在后面看到的，这一点很重要，因为它使得我们可以实现比如递归之类的事情。

¶Beta 规约

Beta 规约才是精彩的地方：这条规则使得 Lambda 演算能够执行任何可以由机器来完成的计算。

Beta 基本上是说，如果你有一个函数应用，你可以对这个函数体中和对应函数标识符相关的部分做替换，替换方法是把标识符用参数值替换。这听起来很费解，但是它用起来却很容易。

假设我们有一个函数应用表达式：“ (lambda x . x + 1) 3 “。所谓 Beta 规约就是，我们可以通过替换函数体（即 “x + 1”）来实现函数应用，用数值 “3” 取代引用的参数 “x”。于是 Beta 规约的结果就是 “3 + 1”。

一个稍微复杂的例子：(lambda y . (lambda x . x + y)) q。这是一个挺有意思的表达式，因为应用这个 Lambda 表达式的结果是另一个 Lambda 表达式：也就是说，它是一个创建函数的函数。这时候的 Beta 规约，需要用标识符 “q” 替换所有的引用参数 “y”。所以，其结果是 “ lambda x . x + q “。

再给一个让你更不爽的例子：“ (lambda x y. x y) (lambda z . z * z) 3 “。这是一个有两个参数的函数，它 (的功能是) 把第一个参数应用到第二个参数上。当我们运算时，我们替换第一个函数体中的参数 “x” 为 “lambda z . z * z “；然后我们用 “3” 替换参数 “y”，得到：“ (lambda z . z * z) 3 “。再执行 Beta 规约，有 “3 * 3”。

Beta 规则的形式化写法为：

1	lambda x . B e = B[x := e] if free(e) subset free(B[x := e])

最后的条件 “if free(e) subset free(B[x := e])” 说明了为什么我们需要 Alpha 转换：我们只有在不引起绑定标识符和自由标识符之间的任何冲突的情况下，才可以做 Beta 规约：如果标识符 “z” 在 “e” 中是自由的，那么我们就需要确保，Beta 规约不会导致 “z” 变成绑定的。如果在 “B” 中绑定的变量和 “e” 中的自由变量产生命名冲突，我们就需要用 Alpha 转换来更改标识符名称，使之不同。

例子更能明确这一点：假设我们有一个函数表达式，“ lambda z . (lambda x . x + z) “，现在，假设我们要应用它：

1	(lambda z . (lambda x . x + z)) (x + 2)

参数 “(x + 2)” 中，x 是自由的。现在，假设我们不遵守规则直接做 Beta 规约。我们会得到：

原先在 “x + 2” 中自由的的变量现在被绑定了。再假设我们应用该函数：

通过 Beta 规约，我们会得到 “3 + 3 + 2”。

如果我们按照应有的方式先采用 Alpha 转换，又该如何？

由 alpha[x/y] 有: (lambda z . (lambda y . y + z)) (x + 2)
由 Beta 规约： (lambda y . y + x + 2) 3
再由 Beta 规约： 3 + x + 2 。

“3 + x + 2” 和 “3 + 3 + 2” 是非常不同的结果！

规则差不多就是这些。还有另外一个规则，你可以选择性地加一条被称为 Eta - 规约的规则，不过我们将跳过它。我在这里描述了一个图灵完备 —— 完整有效的计算系统。要让它变得有用，或看它如何用来做些有实际意义的事情，我们还需要定义一堆能让我们做数学计算的基本函数，条件测试，递归等，我将在下一篇文章讨论这些。

我们也还没有定义 Lambda - 演算的模型呢。（原作者在这里和这里讨论了模型的概念。）模型实际上是非常重要的！逻辑学家们在摆弄了 LC 好几年之后，才为其想出一个完整的模型，这是件非常重要的事情，因为虽然 LC 看起来是正确的，但在早期为它定义一个模型的尝试，却是失败的。毕竟，请记住，如果没有一个有效的模型，这意味着该系统的结果是毫无意义的！

¶ 阿隆佐。丘奇的天才之作 ——lambda 演算中的数字

15 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

所以，现在，让我们用 lambda 演算干点有趣的事。首先，为了方便起见，我将介绍些语法糖（syntactic sugar）来命名函数，以便下面遇到某些复杂的事情的时候方便我们阅读。

引进「全局」函数（即在我写的这些所有的关于 lambda 演算的介绍里都可以直接使用，而不用在每一个表达式中都声明一次这个函数的办法），我们将使用 “let” 表达式：

1	let square = lambda x . x ^ 2

这条表达式声明了一个名为 “square” 的函数，其定义是 lambda x . x ^ 2。如果我们有 “ square 4”，则上面的 “let” 表达式的等效表达式为：

1	(lambda square . square 4) (lambda x . x ^ 2)

某些例子中，我使用了数字和算术运算。但数字并不真正存在于 lambda 演算中，我们有的只有函数！因此，我们需要发明某种使用函数来创建数字的方式。幸运的是，邱奇（Alonzo Church），这个发明了 lambda 演算的天才，找出了做到这一点的办法。他的函数化的数字的版本被称为丘奇数（Church Numerals）。

所有的丘奇数都是带有两个参数的函数：

0 是 “ lambda s z . z “。
1 是 “ lambda s z . s z “。
2 是 “ lambda s z . s (s z)
对于任何数 “n”，它的丘奇数是将其第一个参数应用到第二个参数上 “n” 次的函数。

一个很好的理解办法是将 “z” 作为是对于零值的命名，而 “s” 作为后继函数的名称。因此，0 是一个仅返回 “0” 值的函数；1 是将后继函数运用到 0 上一次的函数；2 则是将后继函数应用到零的后继上的函数，以此类推。

现在看好了，如果我们想要做加法，x + y，我们需要写一个有四个参数的函数；两个需要相加的数字；以及推导数字时用到的 “s” 和 “z”：

1	let add = lambda s z x y . x s (y s z)

让我们将其柯里化，看看是怎么回事。首先，它接受两个参数，这是我们需要做加法的两个值；第二，它需要正则化（normalize）这两个参数，以使它们都使用对 0（z）和后继值（s）的绑定（即，将参数都写成 s 和 z 的组合的形式）。

1	let add = lambda x y . (lambda s z . (x s (y s z)))

看下这个式子，它说的是，为了将 x 和 y 相加，先用参数 “s” 和 “z” 创建（正则化的）丘奇数 “y”。然后应用 x 到丘奇数 y 上，这时候使用由 “s” 和 “z” 定义的丘奇数 y。也就是说，我们得到的结果是一个函数，这个函数把自己加到另一个数字上。（要计算 x + y，先计算 y 是 z 的几号后继，然后计算 x 是 y 的几号后继。）

让我们再进一步看看 2 + 3 的运算过程：

1	add (lambda s z . s (s z)) (lambda s z . s (s (s z))) news newz

为了更容易理解，对数字 2 和 3 做 alpha 变换，“2” 用 “s2” 和 “z2” 代替，3 用 “s3” 和 “z3” 代替：

1	add (lambda s2 z2 . s2 (s2 z2)) (lambda s3 z3 . s3 (s3 (s3 z3)))

用 add 的定义做替换：

1	(lambda x y .(lambda s z. (x s y s z))) (lambda s2 z2 . s2 (s2 z2)) (lambda s3 z3 . s3 (s3 (s3 z3)))

对 add 做 beta 规约：

1	lambda s z . (lambda s2 z2 . s2 (s2 z2)) s (lambda s3 z3 . s3 (s3 (s3 z3)) s z)

然后 beta 规约丘奇数”3”。这步操作其实是 “正则化” 3：把数字 3 的定义里的后继函数和零函数替换成 add 的参数列表里的后继函数和零函数：

1	lambda s z . (lambda s2 z2 . s2 (s2 z2)) s (s (s (s z)))

现在，到了最精妙的一步了。再对丘奇数”2” 做 beta 规约。我们知道：2 是一个函数，它接受两个参数：一个后继函数和 0 (函数)。于是，要相加 2 和 3，我们用后继函数应用到 2 的第一个参数；用 3 的运算结果应用到第二个参数（0 函数）！

1	lambda s z . s (s (s (s (s z))))

于是，我们的结果是：丘奇数”5”！

¶Lambda 演算中的布尔值和选择

15 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

现在，我们在 lambda 演算中引入了数字，只差两件事情就可以表达任意计算了：一个是如何表达选择（分支），另一个是如何表示重复。在这篇文章中，我将讨论布尔值和选择，下一篇将介绍重复和递归。

我们希望能够写出形如 if / then / else 语句的表达式，就像我们在大多数编程语言做的那样。继像丘奇数那样将数字表示为函数之后，我们也将 true 和 false 值表示为对其参数执行一个 if-then-else 操作的函数：

1 2	let TRUE = lambda x y . x let FALSE = lambda x y . y

于是，现在我们可以写一个 “if” 函数，它的第一个参数是一个条件表达式，第二个参数是如果条件为真时才进行运算的表达式，第三个参数则如果条件为假时要进行的运算。

1	let IfThenElse = lambda cond true_expr false_expr . cond true_expr false_expr

此外我们还需要定义常用的逻辑运算：

1
2
3

let BoolAnd = lambda x y . x y FALSE 
let BoolOr = lambda x y. x TRUE y 
let BoolNot = lambda x . x FALSE TRUE

现在，就让我们过一遍这些定义。让我们先看看 BoolAnd：

BoolAnd TRUE FALSE，展开 TRUE 和 FALSE 定义：BoolAnd (lambda x y . x) (lambda x y . y)
alpha 变换 true 和 false：BoolAnd (lambda xt yt . xt) (lambda xf yf . yf)
现在，展开 BoolAnd：(lambda x y. x y FALSE) (lambda xt yt . xt) (lambda xf yf . yf)
beta 规约：(lambda xt yt.xt) (lambda xf yf. yf) FALSE
再次 beta 规约：(lambda xf yf . yf)

于是我们得到结果：BoolAnd TRUE FALSE = FALSE。再让我们来看看 BoolAnd FALSE TRUE：

BoolAnd (lambda x y . y) (lambda x y .x)
alpha 变换：BoolAnd (lambda xf yf . yf) (lambda xt yt . xt)
展开 BoolAnd： (lambda x y .x y FALSE) (lambda xf yf . yf) (lambda xt yt . xt)
beta 规约：(lambda xf yf . yf) (lambda xt yt . xt) FALSE
再 beta 规约：FALSE

所以，BoolAnd FALSE TRUE = FALSE

最后让我们来算算，BoolAnd TRUE TRUE：

展开两个 TRUE： BoolAnd (lambda x y . x) (lambda x y . x)
alpha 变换： BoolAnd (lambda xa ya . xa) (lambda xb yb . xb)
展开 BoolAnd： (lambda x y . x y FALSE) (lambda xa ya . xa) (lambda xb yb . xb)
beta 规约： (lambda xa ya . xa) (lambda xb yb . xb) FALSE
beta 规约： (lambda xb yb .xb)

所以，BoolAnd TRUE TRUE = TRUE

¶ 为什么是 Y？

15 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

在前面的几个帖子里，我已经建立了如何把 lambda 演算变成一个有用的系统的点点滴滴。我们已经有了数字，布尔值和选择运算符。我们唯一欠缺的是重复。

这个有点棘手。lambda 演算使用递归实现循环（递归的解释可以看这里）。但是，由于在 lambda 演算里函数没有名字，我们得采取一些非常手段。这就是所谓的 Y 组合子，又名 lambda 不动点运算符。

让我们先来看看 lambda 演算之外的一个简单的递归函数。阶乘函数，这是标准的例子：

1 2	factorial(n) = 1 if n = 0 factorial(n) = n * factorial(n-1) if n > 0

如果我们要用 lambda 演算来写的话，我们需要几个工具…… 我们需要一个测试是否为零的函数，一个乘法函数，以及一个减 1 的函数。

为了检查是否为零，我们将使用一个命名函数 IsZero，它有三个参数：一个数字，两个值。如果数字为 0，则返回第一个值；如果它不为 0，则返回第二个值。

对于乘法 —— 我们在制定出递归之前写不出乘法。但我们可以假设目前有一个乘法函数 Mult x y。

最后，减 1 函数，我们用 Pred x 表示 x 的前驱 —— 即 x - 1。

所以 —— 第一版的阶乘，如果我们把递归调用留做空白的话，将是：

1	lambda n . IsZero n 1 (Mult n ( something (Pred n)))

现在的问题是，我们怎么填上 “something”，使其递归？

答案是一些所谓的组合子。一个组合子是一种特殊的高阶函数，它们只引用函数应用。（一个高阶函数是一个函数，它接受函数作为参数，并且返回的结果也是函数）。Y 组合子非常特殊，它有近乎神奇的功能使得递归成为可能。它的样子如下：

1	let Y = lambda y . (lambda x . y (x x)) (lambda x . y (x x))

看了公式，你就就明白为什么叫它 Y 了，因为它的 “形状” 像一个 Y。为了让这一点更清晰，有时我们把它写成树的形式。下面是 Y 组合子的树：

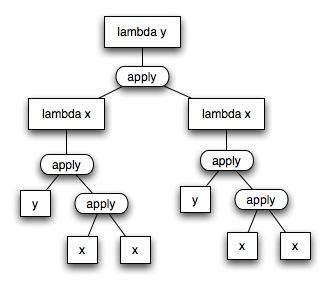
y-combinator

Y 组合子的特别之处在于它应用自身来创造本身，也就是说 (Y Y) = Y (Y Y)。让我们从 (Y Y) 开始看看它如何工作：

Y Y
展开第一个 Y：(lambda y . (lambda x . y (x x)) (lambda x . y (x x))) Y
现在，beta 规约：(lambda x . Y (x x)) (lambda x . Y (x x))
alpha [x/z] 变换第二个 lambda：(lambda x . Y (x x)) (lambda z. Y (z z))
beta 规约：Y ((lambda z. Y (z z)) (lambda z. Y (z z)))
展开前面的 Y，并 alpha[y/a][x/b] 变换：(lambda a . (lambda b . a (b b)) (lambda b . a (b b))) ((lambda z . Y (z z)) ( lambda z . Y (z z)))
beta 规约：(lambda b . ((lambda z. Y (z z)) (lambda z. Y (z z))) (b b)) (lambda b . ((lambda z. Y (z z)) (lambda z. Y (z z))) (b b))

现在，仔细看该表达式。这是 (Y (Y Y)) [记得前面的 (Y Y) = (lambda x . Y (x x)) (lambda x . Y (x x)) 吧]。所以， Y Y = Y (Y Y)，这是 Y 的魔力：它再造了本身。(Y Y) = Y (Y Y) = Y (Y (Y Y))，子子孙孙无穷匮也。

那么，我们如何使用这个疯狂的玩意？

好吧，让我们拿我们的第一次尝试做一下修改。给它取个名字，并尝试使用该名字重写：

1	let fact = lambda n . IsZero n 1 (Mult n (fact (Pred n)))

现在的问题是，“fact” 不是 “fact” 中定义的标识符。我们如何让 “fact” 引用 “fact” 呢？好了，我们可以做一个 lambda 抽象，让 “fact” 函数作为参数传过去；于是，如果我们能找到一种方法来写 “fact”，使得我们可以把它作为一个参数传给它自己，事情就搞定了。我们称之为 metafact。

1	let metafact = lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))

现在，如果我们可以应用 metafact 到本身，我们就得到了我们的阶乘函数。也就是说，

fact n = (metafact metafact) n 。
        <= (lambda f1 . lambda t1 .  t1 ? 1 : t1 * f1 (P(t1))) (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) n  
        <= (lambda t1 .  t1 ? 1 : t1 * (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) (P(t1))) n
        <= lambda n .  n ? 1 : n * (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) (P(n))
        <= lambda n .  n ? 1 : n * (lambda f2 .  P(n) ? 1 : P(n) * f2 (P(P(n))) ) 
        <= lambda n .  n ? 1 : n * (lambda f .  (P(n) ? 1 : P(n) * f (P(P(n))) )
        <= lambda n . n ? 1 : n * (lambda f . f (P(n)))
        <= lambda f . lambda n . n ? 1 : n * f (P(n))
        <= f (n)

这正是 Y 的用武之地。它让我们可以创建一个古怪的结构，每次需要递归的时候都可以复制函数过来。metafact (Y metafact) 将得到我们想要的。展开之，这就是：

1	(lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))) (Y (lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))))

(Y metafact) 实际上是第一个 lambda 中参数 fact 的值；当我们对它做 beta 规约的时候，如果 n 为零，那么它只是返回 1，如果它不为零，那么它调用 fact (Pred n)。然后再将 factbeta 规约为 Y metafact，这个变换疯狂地复制，得到输出 metafact (Y metafact) (Pred n)。

瞧，递归（metafact (Y metafact) = metafact (Y metafact) (Pred n)）。极度扭曲的递归。

我第一次了解了 Y 组合子是在本科，1989 左右，至今我仍然觉得它很神秘。我虽然也明白它是怎么来的，但我无法想象地球上怎么会有人把它给想出来！

如果你对此很长感兴趣，那么我极力推荐「The Little Schemer」这本书。这是本非常棒的小书 —— 写得象一本儿童读物。书里要么每一页正面是一个问题，背面就是答案，要么一页分成两栏，一栏问题一栏答案。书的风格轻松幽默，不仅教你 Scheme 编程，更教人怎么思考。

一个重要的提示：实际上有几个不同的版本的 Y 组合子。也有几种不同的 lambda 演算的计算方式：给定以下表达式：

1	(lambda x y . x * y) 3 ((lambda z . z * z) 4)

我们可以按不同的顺序来计算：我们可以首先对 (lambda x y . x * y) 做 beta 规约，于是有：

1	3 * ((lambda z . z * z) 4)

或者，我们可以先 beta 规约 ((lambda z . z * z) 4)：

1	(lambda x y . x * y) 3 (4 * 4)

在这种情况下，两种方式得到相同的结果；但事实并非总是如此。

第一种顺序就是我们所说的「惰性求值」（Lazy evaluation）：我们不计算函数的参数，直到我们需要使用它们。第二种叫「急切求值」（eager evaluation）：我们总是在把参数传递给函数之前进行计算。（在实际的编程语言中，Lisp 语言，Scheme，和 ML 使用急切求值计算 lambda 演算，Haskell 和 Miranda 则使用惰性值计算 lambda 演算。）我上面描述的 Y 组合子是惰性求值。如果我们用急切求值，那么上述 Y 组合子是导不出来的 —— 事实上，它会永远地复制 Y。

¶ 一点个人解释

¶Y 在定义递归函数中的作用

首先，在 lambda 演算中，函数名不是不可缺少的，没有函数名的函数称为「匿名函数」。lambda 符号的引入就是为了去掉函数名这个冗余，使定义匿名函数成为可能。但是当需要定义的函数含有递归时，比如阶乘 factorial，也就是函数的定义部分需要引用函数自身的时候，没有函数名意味着用 lambda 演算无法直接引用函数自身。怎么办呢？

一种办法是设计另一个函数 G，它接受一个函数作为参数，返回值也是一个函数（这种参数是函数的函数称为高阶函数）。然后，我们把 factorial 当做参数传给 G，如果 G 返回的函数也是 factorial 的话，就圆满了。也就是说，这个 G 需要满足两个特征：

G 的定义中不会出现 factorial，但是它可以接受 factorial 作为参数。回想一下一阶函数 f(x) = x * x，它的定义里没有出现数字「1」，但是「1」可以传给它进行计算。而在构造 G 时，factorial 就相当于数字「1」。
方程 G(f)=f 的解是 factorial。这样我们就不用直接定义 factorial，求解这个关于 G 的方程就可以得到 factorial 的定义了。

于是，我们需要干两件事：找到 G，和找到求解 G(f)=f 的办法。寻找 G 很简单，既然我们想让 G(factorial)=factorial，那么把 factorial 定义中关于 factorial 的引用参数化就可以了，即：

1	let G = lambda f . lambda n . IsZero n 1 (Mult n ( f (Pred n)))

这就是上面的 metafact 函数。这种构造方法可以用于构造任意递归函数的「G」。

然后我们需要找到求解方程 G(f)=f 的办法。满足 f(x)=x 的 x 称为函数 f 的不动点，f 是高阶函数时也不例外。Y 组合子的作用就是计算函数的不动点，它对所有的函数 f 都满足 f(Y(f)) = Y(f)，推理如下：

Y (f) = (lambda y . (lambda x . y (x x)) (lambda x . y (x x))) f
    = (lambda x . f (x x)) (lambda x . f (x x)) 
    = (lambda x . f (x x)) (lambda a . f (a a))
    = f ((lambda a . f (a a)) (lambda a . f (a a)))
    = f ((lambda x . f (x x)) (lambda x . f (x x)))
    = f (Y(f))

于是，factorial 的定义就可以写成：

1
2
3

factorial n = (Y metafact) n 
            = {[lambda y . (lambda t . y (t t)) (lambda t . y (t t))]
               [lambda f . lambda n . IsZero n 1 (Mult n ( f (Pred n)))]} n

这下不用引用自身了。

¶Y 怎么来的

现在回到第一版的阶乘。我们虽然不能直接引用自身，但可以把它作为参数传进来，也就是说：

1	let fact2 = lambda f. lambda n . IsZero n 1 (Mult n ( f (Pred n)))

这样，在计算 5 的阶乘时，我们只需要计算 fact2(fact2, 5) 就可以了。定义并没有引用自身，只是在使用的时候把自己当参数传过去。是不是很简单？

但是，这个计算式是错误的：fact2 的定义要求它接受两个参数，其中参数 f 是只接受一个参数的函数，于是计算式中第二个的 fact2 在参数数量上是无法和定义中的 f 匹配的。那怎么办？

不要紧，我们可以修改一下 f 的形式，让它接受两个参数。即：

1	let fact3 = lambda f. lambda n . IsZero n 1 (Mult n ( f [f, (Pred n)]))

这下计算 fact3(fact3, 5) 就不会出错了。除了这个定义有点丑……

如果对 fact3 做下化简又如何呢？首先是对拥有两个参数的 f 进行柯里化变换：

1 2	let fact3 = lambda h . lambda n . IsZero n 1 (Mult n ( h h (Pred n))) = lambda h . lambda n . IsZero n 1 (Mult n ( (h h) (Pred n)))

这样计算阶乘的方式也相应变成了 (fact3 fact3) 5。接着把 (h h) 用函数 q 代替，则有

1 2	let fact3 = lambda h . lambda n . [lambda q . IsZero n 1 (Mult n ( q (Pred n)))] (h h) = lambda h . [lambda n . lambda q . IsZero n 1 (Mult n ( q (Pred n)))] (h h)

仔细观察中括号部分，参数 h 对于这部分是完全自由的，于是我们可以用另一个函数定义替换之：

1 2	let f0 = lambda n . lambda q . IsZero n 1 (Mult n ( q (Pred n))) let fact3 = lambda h . f0 (h h)

是不是觉得 f0 眼熟？没错，这就是 metafact！不过我们先把 f0 放一边，看看如何使用这个定义计算 n 的阶乘。

1 2	factorail n = (fact3 fact3) n = (lambda h . f0 (h h)) (lambda h . f0 (h h)) n

把上面的式子写成 function_name x 的形式：

1	factorial n = {[lambda f . (lambda h . f (h h)) (lambda h . f (h h))] f0} n

注意大括号中的部分，是不是更眼熟了？这就是 Y 的定义。真是怎么绕都扰不过去的 Y 啊……

1
2
3

factorial n = {[lambda f . (lambda h . f (h h)) (lambda h . f (h h))] f0} n
            = {Y f0} n
            = (Y metafact) n

¶ 从 Lambda 演算到组合子演算

15 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

在昨天介绍了 Lambda 演算中的 Y 组合子（Y Combinator）之后，我认为展示一些你可以用组合子做的有趣的和有用的东西会比较有意思。

让我们来看看三个简单的组合子：

S：S 是一个函数应用组合子： S = lambda x y z . (x z (y z))
K：K 生成一个返回特定常数值的函数： K = lambda x . (lambda y . x)。（即扔掉第二个参数，返回第一个参数）
I：恒等函数： I = lambda x . x

乍一看，这是一个很奇怪的组合。S 的应用机制尤为奇怪 —— 它并不是接受两个参数 x 和 y，并应用 x 到 y，它除了 x 和 y 外还用到了第三个值 z，先将 x 应用到 z 上，再将 y 应用到 z 上，最后用前者的结果应用到了后者的结果上。

这是有道理的。以下各行各做了一步规约：

1
2
3

S K K x = 
(K x) (K x) = 
x

噗！我们根本用不着 I。我们仅用 S 和 K 就创建了 I 的等价。但是，这仅仅是个开始：事实上，我们可以只用 S 和 K 组合子，甚至一个变量都不用，创建任意 lambda 演算表达式的等价。

例如，Y 组合子可以写成：

1	Y = S S K (S (K (S S (S (S S K)))) K)

在我们继续深入之前，有一个重要的事情要指出。我在上面说的是，使用 S K K，我们创建了 I 的等价，然而它并没有规约为 lambda x . x。

到目前为止，我们说在 Lambda 演算中，“x = y”，当且仅当 x 和 y 相同，或通过 Alpha 转化后相同。（这样 lambda x y . x + y 等于 lambda a b . a + b ，但不等于 lambda x y . y + x ）这就是所谓的内涵等价 (intensional equivalence) 。然而，另一种相等也非常有用，这就是所谓的外延等价（extensional equivalence）或外延相等（extensional equality）。外延相等时，表达式 X 等于一个表达式 Y，当且仅当 X 等同 Y（模 Alpha），或者 for all a . X a = Y a。

从现在起，我们使用「=」表示外延相等。我们可以将任何 Lambda 表达式转换为外延相等的组合子形式。我们定义一个从 Lambda 形式到组合子形式的变换函数 C：

C{x} = x
C{E1 E2} = C{E1} C{E2}
C{lambda x . E} = K C{E}，如果 x 在 E 中非自由
C{lambda x . x} = I
C{lambda x . E1 E2} = (S C{lambda x . E1} C {lambda x . E2})
C{lambda x . (lambda y . E)} = C {lambda x . C {lambda y . E}}，如果 x 在 E 中是自由变量

让我们演进一下 C{lambda x y . y x} ：

柯里化函数： C{lambda x . (lambda y . y x)}
根据规则 6： C{lambda x . C{lambda y . y x}}
根据规则 5： C{lambda x . S C{lambda y . y} C{lambda y . x}}
根据规则 4： C{lambda x . S I C{lambda y . x}}
根据规则 3： C{lambda x . S I (K C{x})}
通过规则 1： C{lambda x . S I (K x)}
根据规则 5： S C{lambda x . S I} C{lambda x . (K x)}
根据规则 3： S (K (S I)) C{lambda x . K x}
根据规则 5： S (K (S I)) (S C{lambda x . K} C{lambda x . x})
通过规则 1： S (K (S I)) (S C{lambda x . K} I)
根据规则 3： S (K (S I)) (S (K K) I)

现在，让我们尝试使用 “x” 和 “y” 作为参数传递给该组合子表达式，并规约：

S (K (S I)) (S (K K) I) x y
让我们创建一些别名，以方便阅读：A = (K (S I)), B = (S (K K) I)，所以我们的表达式现在成了：S A B x y
展开 S: (A x (B x)) y
让我们去掉别名 B：(A x ((S (K K) I) x)) y
现在让我们去掉 S：(A x ((K K) x (I x))) y
以及 I：(A x ((K K) x x)) y
规约 (K K) x ：(A x (K x)) y
展开别名 A： ((K (S I)) x (K x)) y
规约 (K (S I)) x ，得到： ((S I) (K x)) y
规约 S：I y (K x) y
规约 I：y (K x) y
最后规约 (K x) y，剩下：y x

就是这样。好玩吧？

¶Lambda 演算的类型

16 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

我们已经掌握了直觉逻辑（Intuitionistic Logic，IL），我们再回到 lambda 演算：我们已经得到了我们需要定义模型的逻辑工具。当然，在没有更简单的事情了，对吧？

到目前为止我们讨论的都是简单的无类型 lambda 演算。一如丘奇首次提出 LC 的第一个版本。但它存在一些问题，为了解决这些问题，人们引入了「类型」（type）的概念，于是出现了简单类型 lambda 演算，之后出现了各种变种 —— SystemT，SystemF，Lambda 立方（和时间立方没啥关系:-)）等等。最终，人们意识到无类型 lambda 演算实际上是类型化 lambda 演算的一个简单到病态的特例 —— 只有一个类型的 LC。

lambda 演算的语义在类型化演算中最容易理解。现在，我们来看看最简单的类型化 LC，叫做「简单类型化 lambda 演算」（simply typed lambda calculus）；以及它如何在语义上等同于直觉逻辑。（其实上，每个种类型化 LC 都对应于一种 IL，而且每个 LC 中的 beta 规约都对应于 IL 中的一步推理，这就是为什么我们需要先跑去介绍直觉逻辑，然后再回到这里。）

类型化 lambda 演算的主要变化是增加了一个叫做「基类型」（base types）的概念。在类型化 lambda 演算中，你可以使用一些由原子值构成的论域（universe），这些值分为不同的简单类型。基类型通常由单个的小写希腊字母命名，然而这正好是 Blogger 的痛处（普通 html 文本打不出希腊字母），我只好用大写英文字母来代替类型名称。因此，例如，我们可以有一个类型「N」，它由包含了自然数集合，也可以有一个类型「B」，对应布尔值 true /false，以及一个对应于字符串类型的类「S」。

现在我们有了基本类型，接下来我们讨论函数的类型。函数将一种类型（参数的类型）的值映射到的第二种类型（返回值的类型）的值。对于一个接受类型 A 的输入参数，并且返回类型 B 的值的函数，我们将它的类型写为 A -> B 。「 ->」叫做函数类型构造器（function type constructor），它是右关联的，所以 A -> B -> C 表示 A -> (B -> C)。

为了将类型应用于 lambda 演算，我们还要做几件事情。首先，我们需要更新语法，使我们可以包含类型信息。第二，我们需要添加一套规则，以表示哪些类型化程序是合法的。

语法部分很简单。我们添加了一个「:」符号；冒号左侧是表达式或变量的绑定，其右侧是类型规范。它表明，其左侧拥有其右侧指定的类型。举几个例子：

lambda x : N . x + 3。表示参数 x 类型为 N ，即自然数。这里没有指明函数的结果的类型；但我们知道，函数「+」的类型是 N -> N ，于是可以推断，函数结果的类型是 N。
(lambda x . x + 3) : N -> N，这和上面一样，但类型声明被提了出来，所以它给出了 lambda 表达式作为一个整体的类型。这一次我们可以推出 x : N ，因为该函数的类型为 N -> N，这意味着该函数参数的类型为 N 。
lambda x : N, y : B . if y then x * x else x。这是个两个参数的函数，第一个参数类型是 N ，第二个的类型是 B 。我们可以推断返回类型为 N 。于是整个函数的类型是 N -> B -> N 。乍看之下有点奇怪；但请记住，lambda 演算实际上只有单个参数；多参数函数的写法只是柯里化的简写。所以实际上这个函数是：lambda x : N . (lambda y : B . if y then x * x else x)；内层 lambda 的类型是 B -> N ; 外层类型是 N -> (B -> N)。

为了讨论程序是否关于类型合法（即「良类型的」(well-typed) ），我们需要引入一套类型推理规则。当使用这些规则推理一个表达式的类型时，我们称之为类型判断（type judgement）。类型推理和判断使我们能推断 lambda 表达式的类型；如果表达式的任一部分和类型判断结果不一致，则表达式非法。（丘奇开始研究类型化 LC 的动机之一是区分「原子」值和「谓词」值，他通过使用类型以确保谓词不能操作谓词，以试图避免的哥德尔式的悖论。）

我将采用一套不太正规的符号表示类型判断；标准符号太难用我目前使用的软件渲染了。常用的符号跟分数有点像；分子由我们已知为真的语句组成；分母则是我们可以从分子中推断出来的东西。我们经常在分子中使用一个叫「上下文」（context）的概念，它包含了一组我们已知为真的语句，通常表示为一个大写的希腊字母。这里我用大写的希腊字母的名称表示。如果一个类型上下文包含声明”x : A，我会写成 CONTEXT |- x : A。对于分数形式的推理符号，我用两行表示，分子一行标有「Given: 」，分母一行标有「Infer: 」。（正常符号用法可以访问维基百科的 STLC 页。）

** 规则 1：（类型标识） **

1 2	Given: nothing Infer: x : A \|- x : A

最简单的规则：如果我们只知道变量的类型声明，那么我们知道这个变量是它所声明的类型。

** 规则 2：（类型不变式） **

1 2	Given: GAMMA \|- x : A, x != y Infer: (GAMMA + y : B) \|- x : A

这是不干涉语句。如果我们知道 x : A，那么我们可以推断出其他任何类型判断都不能改变我们对 x 的类型推断。

规则 3：（参数到函数的推理）

1 2	Given: (GAMMA + x : A) \|- y : B Infer: GAMMA \|- (lambda x : A . y) : A -> B

这个语句使我们能够推断函数的类型：如果我们知道函数参数的类型是 A，而且该函数返回值的类型是 B ，那么我们可以推出函数的类型为 A -> B 。

最后，Rule4：（函数应用推理）

1 2	Given: GAMMA \|- x : A -> B, GAMMA \|- y : A Infer: GAMMA \|- (x y) : B

如果我们知道一个函数的类型为 A -> B ，且把它应用到类型为 A 的值上，那么结果是类型为 B 的表达式。

规则就是这四个。如果我们有一个 lambda 表达式，且表达式中每一项的类型判断都保持一致，那么表达式就是良类型化的（well-typed）。如果不是，则表达式非法。

下面我们找点刺激，描述下 SKI 组合子的类型。这些都是不完整的类型 —— 我用的是类型变量，而不是具体的类型。在真正使用组合子的程序中，你可以找到实际类型来替换类型变量。别担心，我会用一个例子来阐明这一点。

I 组合子： (lambda x . x) : A -> A
K 组合子： (lambda x : A . ((lambda y : B . x) : B -> A)): A -> B -> A
S 组合子： (lambda x : A -> B-> C . (lambda y : A -> B . (lambda z : A . (x z : B -> C) (y z : B)))) : (A -> B -> C) -> (A -> B) -> C

现在，让我们来看一个简单的 lambda 演算表达式：lambda x y . y x。由于没有任何关于类型的声明或参数，我们无法知道确切的类型。但是，我们知道，x 一定具有某种类型，我们称之为 A；而且我们知道，y 是一个函数，它以 x 作为应用的参数，所以它的参数类型为 A，但它的结果类型是未知的。因此，利用类型变量，我们有 x : A, y : A -> B。我们可以通过看分析完整的具体表达式来确定 A 和 B 。所以，让我们用 x = 3，和 y = lambda a : N. a * a 来计算类型。假设我们的类型上下文已经包含了 * 的类型为 “N -> N -> N“。

(lambda x y . y x) 3 (lambda a : N . a * a)
3 是整数，所以它的类型是： 3 : N 。
根据规则 4，我们可以推出出表达式 a * a 的类型是 N，其中 a : N （* 的类型：N -> N -> N），因此，由规则 3，lambda 表达式的类型是 N - > N 。于是，我们的表达式现在变成了：(lambda x y . y x) (3 : N) (lambda a : N . (a * a) : N) : N -> N
所以 —— 现在我们知道，第一个 lambda 的参数 x 须是 N 类型，以及 y 是 N -> N 类型。根据规则 4 我们知道，应用表达式的类型 y x 一定是 N ，然后根据规则 3，表达式的类型为： N -> (N -> N) -> N 。
所以此处的类型 A 和 B 最后都是 N。

所以，现在我们得到了一个简单的类型化 lambda 演算。说它是简单的类型化，是因为这里对类型的处理方式很少：建立新类型的唯一途径就是通过「 ->」构造器。其他的类型化 lambda 演算包括了定义「参数化类型」（parametric types）的能力，它将类型表示为不同类型的函数。

¶ 终章，Lambda 演算建模 —— 程序即证明！

16 Sep 2014 | categories academic
tags 翻译 lambda 演算 function programming

我们已经讲过直觉逻辑（intuitionistic logic）和它的模型；从无类型的 Lambda 演算讲到了简单类型化 Lambda 演算；终于，我们可以看看 Lambda 演算模型了。而这正是真正有趣的地方。

先来考虑简单类型化 Lambda 演算中的类型。任何可以从下面语法生成的形式都是 Lambda 演算类型：

1
2
3

type ::= primitive | function | ( type ) 
primitive ::= A | B | C | D | ... 
function ::= type -> type

这个语法中的一个陷阱是，你可以创建一个类型的表达式，而且它们是合法的类型定义，但是你无法你写出一个拥有该类型的单独的，完整的，封闭表达式。（封闭表达式是指没有自由变量的表达式。）如果一个表达式类型有类型，我们说表达式「居留」（inhabit）该类型，而该类型是一个居留类型。如果没有表达式可以居留类型，我们说这是「不可居留的」（uninhabitable）。

那么什么是居留类型和不可居留类型之间的区别？

答案来自一种叫做「柯里 - 霍华德同构」（Curry-Howard isomorphism）的理论。这种理论提出，每个类型化的 lambda 演算，都有相应的直觉逻辑；类型表达式是可居留的当且仅当该类型是在对应逻辑上的定理。

先看类型 A -> A。现在，我们不把 -> 看作函数类型构造器，而把它视作逻辑蕴涵。A 蕴含 A 显然是直觉主义逻辑的定理。因此，类型 A -> A 是可居留的。

再来看看 A -> B 。这不是一个定理，除非在某个上下文中能证明它。作为一个函数类型，这表示一类函数，在不包括任何上下文的情况下，以 A 类型作为参数，并返回一个不同类型 B。你没法做到这一点 —— 必须有某个上下文提供 B 类型的值 —— 为了访问这个上下文，必须存在某种允许函数访问它的上下文的方式：一个自由变量。这一点在逻辑上和 lambda 演算上是一样的：你需要某种上下文建立 A->B 作为一个定理（在逻辑上）或可居留的类型（在 lambda 演算上）。

下面就容易理解些了。如果有一个封闭 LC 表达式，其类型是在相应的直觉逻辑中的定理，那么，该类型的表达式就是定理的一个证明。每个 Beta 规约则等同于逻辑中的一个推理步骤。对应于这个 lambda 演算的逻辑就是它的模型。从某种意义上说，lambda 演算和直觉逻辑，只是同一件事的不同反映。

有两种方式可以证明这个同构：一种是柯里当初采用的，组合子演算的方式；另一种则用到了所谓的「相继式演算」（Sequent calculus）。我会组合子证明的版本，所以下面我会快速的过一遍。以后，很可能下个礼拜，我会讲相继式演算的版本。

让我们回忆一下什么是模型。模型是一种表示演算中的每条声明（statement）在某些具体值域上都合法的方式 —— 所以存在具体实体和演算中的实体的对应关系，凡演算中的声明都对应真正的实体的某些声明。所以我们实际上并不需要做充分的同构；我们只需要一个从演算到逻辑的同态（homomorphism）。（同构是双向的，从演算到逻辑和逻辑到演算；而同态只从演算到逻辑。）

所以我们需要做的是取任意完整的 lambda 演算表达式，然后将其转化为一系列合法的的直觉逻辑语句。由于直觉逻辑本身已被证明是合法的，如果我们可以把 lambda 演算翻译成 IL，这样我们就证明了 lambda 演算的合法性 —— 这意味着我们将表明，在 lambda 演算中的计算是合法的计算，以及 lambda 演算是一个完全的，合法的，有效的计算系统。

我们如何从组合子（它们只是省去了变量的 lambda 演算的简写）得到直觉逻辑？它实际上简单得令人难以相信。

直觉逻辑中的所有证明可以归结为一系列的步骤，其中的每一步都是使用了以下两个基本公理之一的推理：

A implies B implies A
(A implies B implies C) implies ((A implies B) implies (A implies C))

让我们用箭头重写它们，让它们看起来像一个类型：A -> B -> A ；及 (A -> B -> C) -> ((A -> B) -> (A -> C))。

眼熟吗？不熟的话再回头看看简单类型化 lambda 演算。这就是 S 和 K 组合子的类型。

接下来的建模步骤就很明显了。lambda 演算的类型对应于直觉逻辑的原子类型。函数是推理规则。每个函数可以规约为一个组合子表达式；每个组合子表达式是直觉逻辑的某个基本推理规则的实例。于是，函数就成了相应逻辑里的定理的一个构造性证明。

酷吧？

（任何正常人看完会说 “什么？”，但，我显然不是正常人，我是一个数学怪咖。）

¶ 博客推荐：good math, bad math 之 Lambda 算子简介

Good math，bad math 是我最近发现的一个博客。作者 Mark Chu-Carroll 写的一系列关于计算机科学理论的文章深入浅出，通俗易懂，属于茶余饭后绝佳的消遣读物。俺一直想写点介绍 lambda caculus 的小文章，但看了他的 “My Fravorite Calculus: Lambda” 后，就打消了这个念头。有这么好的文章，转贴就行了，自己就不用再写不入流的文章。今天先转介绍 lamdba calculus 的第一部分。先申明一下，俺的翻译在不影响作者原意的基础上（但愿能做到到），有时也插科打诨加点 8 卦。如果谁觉得文章垃圾，完全因为俺水平有限。原文绝对精彩。另外，俺数学方面的术语止于大一微积分。所以术语用错了，还请多多指正。

在计算机科学尤其是是编程语言领域，我们常用一种算子：Lambda Calculus。逻辑学家也常用 Lambda Calculus 来研究计算和离散数学结构的本质。其实当初 Alanzo Church(就是丘奇 - 图灵论点里的那位丘奇老大了）和 Stephen Cole Kleene(就是自动机理论里 Kleene Star 那个 Kleene 了）推出这个 Lambda Calculus，也是为了方便他们做逻辑方面的推理，好证明决定性问题。当然以 Church 和图灵的天才，没多久他们便证明图灵机和 lambda calculus 具有等价的计算能力。Church 提出 Lambda Calculus 时就怀疑他的理论能被用在其它地方。事实证明他的确高瞻远瞩。Lambda Calculus 在编程的理论和实践两方面都意义深远。做理论和做函数编程的且不说。就算是玩儿脚本语言的老大们，也多半成天和 lambda 打交道。说来好玩儿，计算机科学理论的发展相当诡异。常常是逻辑学家为了推进逻辑理论提出一个理论，若干年后计算机科学家出于实际需求再 “重新发现” 一模一样的理论。比如说现在很多函数编程语言常用的 Hindley-Milner 类型系统，就是逻辑学家 Roger Hindley 于 1969 年先发现，再由大名鼎鼎的牛人 Robin Milner 于 1978 年独立提出。说远了。Lambda Calculus 本身有若干显著优点：

它非常简单。反正比图灵机简单。
它图灵完备。也就是说，图灵机能完成的计算，Lambda Calculus 也能完成。
它易于读写。这点很重要。简单就是力量。我们不可不记。
它的语义足够强大，能让我们用它来推理。
它的计算模型足够强大
容易创建不同的变种，以便我们探索用不同的方式构建计算或语义时的特性

Lambda Calculus 易于读写意义重大。正是这个优点催生了许多或多或少基于 lambda calculus 的极为优秀的编程语言：Lisp, ML, 和 Haskell 都在很大程度上基于 Lambda calculus 开发出来。

Lambda calculus 建立在函数这个概念上。纯粹的 lambda 算子理论中，任何东西都是函数。除了函数外别无它物。不过我们可以用函数搭建出各种东西。其实我们可以从 lambda calculus 开始，从无到有搭建出整个数学的结构。

牛皮轰轰吧？我们就来看一下 lambda calculus 为什么这么神奇。对任何一个算子理论来说，我们必须先定义两个东西。一是句法 (syntax)，用来描述什么表达式是合法的；二是一套规则，用来规定我们怎么对表达式作合法的符号操作。

¶Lambda Calculus 句法

Lambda calculus 只有三种表达式

函数定义：在 lambda calculus 里一个函数就是一个表达式，写成 lambda x . <函数体>。意思是 “一个函数，带一个参数 X，返回计算函数体后得到的结果”。这个时候我们说这个 lambda 表达式绑定了参数 X。
标识符引用（identifier reference): 一个标识符引用就是一个名字。这个名字和包括这个引用的函数定义里的参数同名。
函数应用 (function application): 这个更简单，把要应用的值放到函数定义的后面就行了。比如
(lambda x . plus x x) y

这么简单的定义能干什么嗫？怎么没有多个参数嗫？这个就是数学的魅力了。我们很快会发现，多个参数可以被等价的操作（所谓的 currying) 来代替。而配上简单的操作后（本质操作就一个：替换），我们就得到了一门强大的编程语言，不输基于图灵机模型的 Algo 系列语言，比如 C。

欲知后事如何，且听下回分解。

¶lambda 算子简介 1.a

接着前两天的转载继续写。上次说到 lambda 算子的函数只接受一个参数。那怎么处理多个参数呢？如果只有一个参数，那岂不是连加法都不能实现？这当然难不倒像丘齐这样的天才。于是， lo and behold, 一个我们至今在编程里常用的技巧粉墨登场：

¶Currying

据说 Currying 翻译为局部套用函数，也不知真假。喜欢吃印度美食的老大们不要激动。Currying 和咖喱没有半点关系。这个技巧以逻辑学家 Haskell Curry 的姓命名。Haskell Curry 也是名动一时的人物。他和 Moses Schönfinkel 共创了组合逻辑（combinatory logic)，并把这们学科发扬光大。当初 Curry 搞出组合逻辑，主要是为了在数理逻辑里避免使用变量。后来搞函数编程的人们发现，组合逻辑是一类函数编程语言的理论基础。一些函数语言里常见的特性，比如说高阶函数合 lazy evaluation, 就是用组合逻辑里的 combinator 实现的。当初 Alanzo Church 对这个理论也相当熟悉。难说 lambda 理论不是受了组合逻辑的影响。大牛 Philip Wadler 为了纪念 Curry, 把他的函数语言叫做 Haskell。Haskell 也是一门巨酷的函数语言，兼顾数学的优美和软件开发的实用性。连 LInspire 的开发组都决定用 Haskell 作为系统开发的语言（但我很奇怪他们为什么放弃使用另一门酷酷的函数语言 Ocaml）。说远了。

解决参数限制的关键在于认识到函数也是数据（用更严格的说法，是值）。既然是数据，就可以传来传去。如果有两个参数，我们可以写一个接受第一个参数的函数，而这个函数返回的是接受第二个参数的函数。“就那么简单！我们在 JavaScript 里不是常用这个功能？” 嘻嘻，我们在 JavaScript 里的确常用这个功能。JavaScript 其实是带 C 句法的函数语言，支持高阶函数，自然支持 Currying。JavaScript 的功能其实颇为强大，不然 Douglas Crockford 不会说 JavaScript 是最被人误解的语言。

举例来说，假设我们要写一个函数，把 x 和 y 相加。最自然的写法是 lambda x y . plus x y. 既然我们只能一次接受一个参数，我们可以先写一个接受 x 的函数。这个函数返回一个接受 y 的函数。这个被返回的函数把 x 和 y 相加：lambda x.(lambda y. plus x y)。简单吧？数学奇妙之处就在于我们用极为简单的砖块搭建出恢弘的宫殿。事实上，数学家们总是极力追求理论基础的简洁。他们不知疲倦地挥舞着奥卡姆剃刀，直到把自己的理论切割成东家之子：增之一分则太长，减之一分则太短。有了 Currying 这个工具，我们可以放心使用多参数的标记了。反正多参数的 lambda 不过是单参数 lambda 的方便用法而已，没有任何实质上的改变。

（待续。累死了。什么时候才能写到让人拍案叫绝的 Y Combinator 啊？)

¶lambda 算子 1.b

¶ 自由 vs 有界标识符

标识符和变量其实是一个意思。我记得国内教材里很少用标识符这个说法。不过既然原作者用这个说法，我就跟着用了。上次说到 Currying 解决了如何处理多参数的问题。在讨论怎么使用 lambda 前，我们还要解决一个细微但重要的语法问题：封闭 (closure)，或者叫完全有界 (complete bounding)。这里的有界和一阶谓词逻辑里的有界没有本质区别，对一阶谓词逻辑熟悉的老大们可以放心跳过。其实有界涉及的定义很直观，我们看一个例子先。假设我们有一个函数 lambda x y. (lambda y. y + 2) + x + y +z，lambda y. y+2 里的 y 和它后面的 y 是不是一样的呢？显然它们是不一样的。为了处理这种区别，我们引入了有界。当一个 lambda 表达式被计算时，它不能处理无界的标识符。当一个标识符出现在一个 lambda 表达式的参数里，并且被包含在这个 lambda 表达式里，我们就可以说这个标识符有界。如果一个标识符没有被包含在任何一个表达式里，我们就叫它为自由变量。比如说，上面那个 lambda 表达式里，x 出现在 lambda x y .(....) 里，所以它是有界的变量，它的包含环境（enclosing context，用 “语境” 或者 “上下文” 怎么听怎么别扭，好像俺是《读书》的御用作者似的。😄) 是整个 lambda 表达式。lambda y. y+2 里的 y 也是有界的，但它的包含环境是 lambda y. y+2。标识符 z 没有出现在包含它的表达式的参数列表里，所以是自由变量。再举几个例子：

lambda x . plus x y: 这个表达式里，"y" 和 "plus" 都是自由变量，因为它们不是任何包含它们的表达式的参数。x 有界，因为它被包含在 plus x y 里，而 plus x y 的参数有 x。
lambda x y.y x: 这个表达式里，x 和 y 都有界，因为它们是这个表达式的参数。
lambda y . (lambda x . plus x y): 在内嵌的表达式 lambda x. plus x y 里，y 和 plus 是自由变量而 x 是有界变量。在整个 lambda 表达式里，x 和 y 都有界：x 在内嵌表达式界内，而 y 在整个表达式界内。plus 仍然自由。

我们用 "free (x)" 来代表表达式 x 里所有自由变量的集合。

一个 lambda 表达式完全合法仅当它的所有变量都有界。不过当我们考查某个复杂表达式里的子表达式且不考虑上下文时，那些子表达式可以有自由变量－其实确保正确处理那些子表达式里的自由变量非常重要。

¶Lambda 算子计算规则

其实真正的规则就俩：alpha 和 beta。Alpha 规则又叫转换 (conversion) 规则，而 beta 规则又叫简化 (reduction) 规则。

¶Alpha 转换

这个充满了《星际迷航》味道的规则其实就是重命名操作。它无非是说变量名不重要：给定任何一个 lambda 表达式，我们可以任意改变参数的名字，只要我们相应地改变这些对应这些参数的变量名字。

比如说，我们有如下表达式：
lambda x . if (= x 0) then 1 else x^2

我们通过 alpha 规则把 X 改成 Y（写作 alpha [x/y], 和逻辑里的变量替换一个写法），于是得到：
lambda y . if (= y 0) then 1 else y^2

Alpha 操作完全不影响 lambda 表达式的意义。不过我们后面会发现，这个操作很重要，因为它让我们能够实现诸如递归的操作。

¶Beta 简化

Beta 简化就有意思了。我们只需要这一个规则，就可以让 lamdba 算子实现一台计算机能做的任何计算。透过纷繁的表象，我们会发现事情的本质往往出人意料地清晰而简单。删繁为简，恰是数学魅力所在。

Beta 规则无非是说，应用一个函数 (也就是 lambda 表达式。一个意思）等价于通过把函数体内有界的变量替换成应用里对应参数的实际值来替换原来的函数。听上去有些拗口（呵呵，其实原文更拗口），但当你看一个例子就知道它其实很简单：

假设我们要应用一个函数：“(lambda x . x + 1) 3”。Beta 规则说，我们可以替换整个表达式，把函数体（也就是 “x+1”) 里的参数对应的 x 替换成实际的值 3。所以最后的结果是 “3＋1”。

再来一个稍微复杂点的例子：
lambda y . (lambda x . x + y) q

这个表达式有意思，因为应用了这个表达式后，我们可以得到另外一个表达式。也就是说，它是一个生成表达式的表达式（说到这里，玩儿动态语言的老大们可以笑了，玩儿 C/C++/Java 的老大们可以流口水了）。当我们对这个表达式应用 Beta 简化时，我们把所有对应参数 y 的变量替换成实际的值 q。所以结果是 "lambda x, x+q"。

再来一个例子：
“(lambda x y. x y) (lambda z . z * z) 3”. 这个带两个参数的函数把第一个参数应用到第二个参数上。当我们计算它的值时，我们把第一个 lambda 表达式里的变量 x 换成 lambda z. z * z, 再把变量 y 换成 3，得到 (lambda z. z * z) 3。对该结果应用 Beta 简化，我们得到 3 * 3。

Beta 的严格定义如下：

lambda x . B e = B[x := e] if free(e) /subset free(B[x := e]

这个定义末尾的条件，"if free (e) /subset free (B [x:=e])" 道出了我们需要 Alpha 转换的原因：仅当 beta 化简不会引起有界变量和自由变量的冲突时，我们可以实施 Beta 化简。如果一个变量 “z” 是 "e" 里的自由变量，那我们得保证 beta 化简不会让 "z" 变成有界变量。如果 B 里的有界变量和”e" 里的自由变量重名，我们必须先用 Alpha 转换，是的重名的变量不再重名。形式化定义不够直观，直观描述又不够简洁。还是来个例子漱漱口：

给定一个表达式，lambda z. lambda x. x+z. 假设我们要应用这个表达式：
(lambda z . (lambda x . x + z)) (x + 2)

在实际参数 "(x + 2)" 里，x 是自由变量。但 x 不是表达式 lambda x. x+z 的自由变量。也就是说，free (e) /subset free (B [ x:=e]) 不成立。如果我们打破 Beta 简化的规则，直接开始 Beta 简化，便会得到: lambda x . x + x + 2

"x+2" 里自由变量，x，现在变得有界了。如果我们把结果应用到 3 上：(lambda x. x+2+2) 3，我们得到 3 + 3 + 2。

如果我们按正常程序办事呢？

应用 alpha [x/y]: lambda z . (lambda y . y+z)) (x + 2)
应用 beta: lambda y . y + x + 2) 3
再次应用 beta: 3 + x + 2.

“3+x+2” 和 “3+3+2” 很不一样哈！

规则就这些了。我们还可以选择性地加一个所谓的 Eta - 化简，不过它不是必需的。我们就此跳过。我们讨论的这套系统已经是图灵完备的计算体系。那这套系统到底有什么用嗫？到底怎样才能让这套系统变得真正有用嗫？嗯，要说明这些问题，我们得先定义一些基本的函数，以便我们做算术，条件测试，递归，等等。这些会在以后的帖子里谈到。

我们也还没有谈到适合 lambda 算子的模型（Good Math Bad Math 的作者在这里和这里讨论了模型）。模型也是很重要的东西。逻辑学家用了好几年时间研究 lambda 算子，才搞出一个完备的模型。而且早先时候，尽管 lambda 算子看起来没错，为它制订模型的工作却失败了。这在当时极为引人关注。要知道，毕竟一个系统没有有效的模型就没有实际的意义。

¶lambda 算子 3: 阿隆佐。丘齐 (Alonzo Church) 的天才

前面建立了 lambda 运算的基本规则，就可以用 lambda 算子做点有意思的东西了。开始前为方便计，我们先来点语法糖花差花差，用来命名函数。这些语法糖可以让复杂的公式好写一点。

我们用 "let" 来引入一个 “全局” 函数（也就是说，我们用这个函数时，不用在每个表达式里定义一次）：
let squer = lambda x. x^2

这个式子申明了一个叫 "square" 的函数，定义为 lamdba x. x^2。如果我们有一个表达式 “square 4”，上面的 "let" 意味着这个表达式和下面这个表达式一样：(lambda square. square 4)(lambda x. x^2)。这个 "let" 是从 Common Lisp 或者 Scheme 里借来的。Lambda 算子里可没有这个东西。数学家推崇 “如无必要，毋增实体”。这些关键字不入他们的法眼。不过对写惯了程序的我们来说，这些句法糖就可爱多了。

我们的例子里会用到数字和算术操作符。不过记住 lambda 算子里根本没有数字。我们只有函数！所以我们需要发明用函数来创造数字的方法。幸好 Alonzo Church 是个天才。他既然发明了 lambda 算子，用 lambda 算子表征数字自然不在话下。他搞出的用于数字的函数自然就叫做丘齐数（Church Numerals)。

丘齐数里，所有的数字都是两个参数的函数：

零是 lambda s z . z
一是 lambda s z . s z
二是 lambda s z . s (s z)
对任意一个数 "n"，它的丘齐数都是一个函数。这个函数把它的第一个参数应用到第二个参数上 n 次。用流行的写法，就是 lambda s z . s sn z。绕口啊绕口。做形式化的东东不幸之处就是成天和绕口令打交道。解脱这道呢？当然就是牢记牛人费因曼在 Connection Machine 工作时的学习方法：问最简单的问题。“给我最简单的例子”。“怎么才能验证这是正确的？”。比如说零（lambda s z . z）吧，第一个参数是 s, 应用零次就是没有，所以函数体就是孤零零的 "z"。那数字一呢？当让就是把第一个参数，s，应用到 z 上一次，所以函数体就变成了 "s z"。

理解这个定义的方法之一时把 "z" 看作丘齐数里零的名字，而把 "s" 看后继函数（successor function) 的名字。“后继函数” 其实很简单，C/C 里的是也。所以呢，零就是一个返回 "0" 这个值的函数；一就是把后继函数应用到零上一次的函数；二就是把后继函数应用到一上一次或者说零上两次的函数。0++ 得到 1, 1++ 等价与 (0++)，而 1 得到 2．现在把 0 换成 z，把 ++ 换成 s, 一切就清楚了。

现在－－看好了。如果我们想做加法，x+y，我们需要一个带 4 个参数的函数。两个参数代表相加的两个数字，以及为得到结果而需要的 "s" 和 "z"。

let add = lambda s z x y . x s (y s z)

看着好像有点不知所云。不过我们可以用 Curry 这个利器，分开 "s" "z" 和 x, y。首先，Curry 后得到的函数带两个参数，x 和 y（这个好比 add (x, y)，符合我们对加号的理解）。其次，我们需要正规化 x 和 y 需要的 s 和 z，让 x 和 y 共享相同的零和后继函数的绑定：

let add = lambda x y. (lambda s z . (x s (y s z)))

仔细观察一下，上面的式子无非是说，要把 x 和 y 相加，我们先用 "s" 和 "z" 创建丘齐数 "y"，然后在把 "x" 应用到 y 上。应用时需要的 "s" 和 "z" 是 "y" 里的 "s" 和 "z"。也就是说，我们的到的结果是一个函数，这个函数把自己加到另一个函数上。还是用例子来说明问题。比如说 2+3:

add (lambda s z. s (s z)) (lambda s z . s (s (s z))) news newz

为了让演算变得稍微容易一点，我们先对 2 和 3 来个 Alpha 转换。让 2 用 s2 和 z2，而 3 用 s3 和 z3:

add (lambda s2 z2 . s2 (s2 z2)) (lambda s3 z3 . s3 (s3 (s3 z3)))

现在我们可以把 "add" 替换成它的定义了：

(lambda x y .(lambda s z. (x s y (s z)))) (lambda s2 z2 . s2 (s2 z2)) (lambda s3 z3 . s3 (s3 (s3 z3)))

现在可以对 "add" 用 beta 变换了（温馨提示：也就是把形参 x 和 y 换成对应的实参）：

lambda s z . (lambda s2 z2 . s2 (s2 z2)) s (lambda s3 z3 . s3 (s3 (s3 z3)) s z)

然后我们可以对 3 这个丘齐数做 beta 转换。这步操作其实是 “正规化” 3：把 3 的定义里的后继函数和零函数（还记得零是个函数吧？）替换成 add 的参数列表里的后继函数和零函数：

lambda s z . (lambda s2 z2 . s2 (s2 z2)) s (s (s (s z)))

嗯，有点眉目了。现在是真正漂亮的地方了。再来次对 2 的 Beta 变换。看看我们准备做什么：2 是个带两个参数的函数：一个参数是后继函数，另一个是零函数。要把 2 加到 3 上，我们只需要用到 "add" 这个函数的后继函数。也就是说，我们把计算了 3 后的结果当成零函数的值！

lambda s z . s (s (s (s (s z)))

而这个式子，正是丘齐数 5！

丘齐数酷的地方是它抛弃了传统整数的概念，用函数取而代之。它把每个数对应为一个函数。而数数（counting）这个操作被对应为应用某个函数（在这里是后继函数）的次数。当然了，上面的介绍非常简单。对丘齐数感兴趣的，可以看这篇文章。

丘齐数对编程有什么用嗫？俺还真不知道。但丘齐数（进而到丘齐编码）确实一系列基础理论中有重要应用，比如说有类型的 lambda 算子。不过这点重要吗？不重要吗？重要吗？不重要吗？研究研究嘛。

¶lamdba 算子 4：布尔值和选择

¶Lambda 算子里的布尔值和选择

原文在这里。既然 Lambda 算子里有了数的概念，我们想进行任意的计算就只需要两件东西了：怎么表示选择，和怎么表达重复操作。我们先聊聊怎么表示布尔值（也就是非真即假的二元集合）和选择，然后再讨论重复和递归（友情预告：人见人爱的 Y Combinator 终于可以出场了）。

我们一般把选择表示为 if/then/else 的表达式，和大多数编程语言的选择语句没有区别。丘齐数的基本模式无非是把一个数表达为一个函数。这个函数把它自己加到另外一个函数上。我们继续沿用这个模式，把 true 和 false 也表达为对自己的参数执行 if-then-else 操作的函数：
let TRUE = lambda x y . x
let FALSE = lambda x y . y

现在我们就可以写 “if-then-else” 函数了（记到哈，lambda 算子理论里所有东东都是函数）。这个函数的第一个参数是一个条件表达式，第二个参数是当第一个参数为真时返回的表达式，而第三个参数自然是当第一个参数为假时返回的表达式了。相当于我们的 if cond then true_expr else false_expr:
let IfThenElse = lambda cond true_expr false_expr . cond true_expr false_expr

为了我们刚定义的布尔值有用，我们还得定义一些常用的逻辑操作先：
let BoolAnd = lambda x y . x y FALSE
let BoolOr = lambda x y. x TRUE y
let BoolNot = lambda x . x FALSE TRUE

上面定义了常用的 “与”，“或”，和 “非” 操作。我们可以稍微考查一下它们的机制。

BoolAnd TRUE FALSE （也就是 true && false)：

我们把 TRUE 和 FALSE 替换为它们的定义: BoolAnd (lambda x y . x) (lambda x y . y)
执行 Alpha 替换避免混淆变量名：BoolAnd （lambda xt yt . xt) (lambda xf yf . yf) 然后把 BoolAnd 替换为它的定义：（lambda x y . x y FALSE）(lambda xt yt . xt) (lambda xf yf . yf) 执行 Beta 替换：(lambda xt yt . xt) (lambda xf yf . yf) FALSE 呵呵，再 Beta 一把：(lambda xf yf . yf)。

最后的结果 lambda xf yf . yf 就是 FALSE 的定义。也就是说， BoolAnd TRUE FALSE = FALSE。神奇吧？看起来只是简单的替换：变量替换，参数替换，但最后的结果确意义重大。这让我想起当年第一次读 GEB 时不由自主地感叹，看似简单的句法层面的操作竟然能得出迷幻般的结果。

我们再来看看 false && true, 也就是 BoolAnd FALSE TRUE。“噫，那不是和我们刚推演过的BoolAnd TRUE FALSE 一样么！”。眼尖的老大们可能要问。嗯，我们知道布尔逻辑里的操作是服从交换率的，所以 a && b 等于 b && a。可惜我们在用 lambda 算子定义布尔操作，是不是服从交换率，需要我们证明。如果 BoolAnd FALSE TRUE 的结果是 FALSE，我们也就证明了 BoolAnd 符合交换率：定义替换：BoolAnd (lambda x y . y) (lambda x y .x)
Alpha 替换: BoolAnd (lambda xf yf . yf) (lambda xt yt . xt)
替换 BoolAnd 的定义: (lambda x y .x y FALSE) (lambda xf yf . yf) (lambda xt yt . xt)
Beta 替换: (lambda xf yf . yf) (lambda xt yt . xt) FALSE
再来 Beta 替换: lambda xt yt. xt, 也就是 FALSE
所以说， BoolAnd FALSE TRUE = FALSE

最后，我们来看看 BoolAnd TRUE TRUE:
定义替换：BoolAnd (lambda x y . x) (lambda x y . x)
Alpha 替换: BoolAnd (lambda xa ya . xa) (lambda xb yb . xb)
替换 BoolAnd 的定义: (lambda x y . x y FALSE) (lambda xa ya . xa) (lambda xb yb . xb)
Beta 替换: (lambda xa ya . xa) (lambda xb yb . xb) FALSE
再次 Beta 替换: (lambda xb yb .xb)，这个正是 TRUE 的定义所以我们得到 BoolAnd TRUE TRUE = TRUE

¶Lambda 算子 5b：How of Y

其实是这篇文章的意译。有些东西省了。添了点私货。就有了下面的帖子。虽然 Y 相当神奇。对它的推导也不完全是天外飞仙般无迹可寻。基本上我们为了解决让没有名字的函数能自我引用，一步一步抽象出了 Y。所以知道 Y 的推导过程对我们程序员还是很有意义的：毕竟编程的过程也是抽象的过程。看看当年的老大们怎么从纷繁的表象里抽象出一般规律，对我们日后的思考应该大有好处。为了老大们能够试验，我就用 JavaScript 了。整个推导的过程非常像编程时的重构。我们提出一个粗略的解决方案，然后仔细观察，找出可以抽象的地方，进行抽象。得到一个更普适的结果后，继续重复重构的步骤，直到得到最优解。估计看这篇帖子的人都知道怎么玩儿小小 JavaScript 吧？再说有个浏览器就有了测试环境。废话少说，看代码。我们还是以阶乘函数为例。先看通常的写法：

function fact(n){
        if(n == 0){
                return 1;
        }

        if(n > 0){
                return n * fact(n - 1);
        }
}

上面的 JavaScript 函数定义内部调用自己。这种调用可行的前提是我们用函数名指代函数定义。也就是说， fact 这个名字绑定的函数定义就是上面的函数体。如果我们不能通过名字来调用函数怎么办呢（就跟 lambda 算子一样）？也许有老大会问：为什么增加这个限制呢？不是自虐么？理由很简单：理论需要探求事物本质。记得奥卡姆剃刀吧？如无必要，毋增实体。函数名到底是必需元素，还是句法糖？这种研究方法也有实际的意义：再复杂的系统也是在简单但完备的基础上搭建起来的。强大的编程工具，总是基于于层层叠加的抽象，而最低级的抽象层总是非常简单。简单意味着透彻，简单意味着健壮。简单意味着灵活。简单意味着经济。问题是，到底简单到什么地步？怎么保证系统不至于简单到一无所用的地步？这和逻辑学家建立系统时总是要证明系统的正确性和完备性一个道理。而找到了 Y，我们也就明白了，原来函数名绑定并非本质。

嗯，继续。函数 fact 是递归的基本形式。既然我们不能直接在函数体内通过函数名调用另一个函数，我们至少可以把想调用的函数通过参数传进去。

References